除法竖式计算是数学中一项基础而重要的技能,其过程从基础到实践的全面解析如下:,1. 确定被除数和除数:被除数是被除的数,除数是用于去除的数。,2. 计算商:将除数与被除数的最高位数字相除,得到商的个位数。,3. 计算余数:将上一步的余数与被除数的下一位数字组合,再与除数相除,得到新的商和余数。,4. 重复步骤3,直到余数为0或达到所需精度。,5. 记录商的每一位数字:从左到右依次记录每次得到的商的数字。,6. 注意事项:在计算过程中,要确保每次除法运算的准确性,避免出现错误,要注意余数的处理,确保其小于除数。,通过以上步骤,可以掌握除法竖式计算的基本方法和技巧,提高数学运算的准确性和效率。
在小学数学中,除法是一个基础而重要的概念,它不仅是日常生活中的实用技能,也是更高层次数学学习的基石,掌握除法竖式计算过程,不仅能够帮助孩子们建立扎实的数学基础,还能培养他们的逻辑思维和问题解决能力,本文将详细介绍除法竖式计算的基本原理、步骤以及实际应用,旨在为读者提供一个清晰、易懂的学习指南。
除法的基本概念
除法是四则运算之一,其目的是将一个数(被除数)分成若干等份,每份的数量相同(即除数),并求出可以分成几份(商)以及每份的剩余(余数),在竖式计算中,这一过程通过逐步减法和除法运算的视觉化展示来体现。
除法竖式计算的基本步骤
-
准备阶段:将除数(通常为较小的数)写在被除数(较大的数)的左侧,作为除法的起始点,确保被除数和除数的位置正确,被除数在上方,除数在下方。
-
首次除法:从被除数的最高位开始,用除数去除以它,得到商的第一个数字,这个过程中,可能需要考虑除数的倍数来决定商的初始位置,如果用7去除以123(假设123为被除数),则首先考虑7的倍数,发现7×18=126,但123小于126,所以商为0,然后考虑7×17=119,发现123-119=4,所以商的第一个数字是17的个位7。
-
逐位相减:将上一步得到的商与除数相乘,并将结果从被除数中减去,继续这个过程直到被除数的某一位小于除数为止,在上述例子中,继续用7×7=49减去4(上一步的余数),得到0,这意味着我们已经成功地将123完全除以7。
-
记录余数:如果最后还有余数(即被除数减去所有已减去的部分后剩余的数字),则将这个余数作为本次除法的结果的一部分,在上述例子中,由于最终余数为0,所以商为17(即7×17=119),没有余数。
-
重复过程:如果被除数包含小数点后的数字(即不是整数),或者需要更精确的商(如带余数的长除法),则重复上述步骤,每次从被除数的下一位开始新的除法过程。
实际应用与注意事项
-
实际应用:除法竖式计算在日常生活和工作中非常实用,在购物时计算找零、在烹饪中按比例调配食材、在财务管理中分配资金等,掌握这一技能能让人在处理实际问题时更加得心应手。
-
注意事项:
- 确保每次相减后余数小于除数,这是避免错误的关键。
- 理解并记住“借位”的概念,特别是在处理多位数的减法时。
- 练习是提高的关键,通过大量的练习,可以增强对除法竖式计算过程的熟练度和准确性。
- 理解“商”和“余数”的概念对于解决复杂问题至关重要。
- 遇到困难时,可以尝试使用“试商”的方法,即先估计一个商的近似值,然后根据实际情况调整。
教学与学习建议
对于学生而言,学习除法竖式计算时可能会遇到一些挑战,尤其是对初学者来说,理解每一步的逻辑和意义尤为重要,以下是一些教学与学习建议:
- 使用教具:利用实物(如小棒、积木)来模拟除法过程,帮助学生直观理解“分”的概念。
- 分步讲解:教师或家长应分步解释每一步的意图和目的,确保学生理解每一步的逻辑基础。
- 练习册与游戏:利用练习册进行大量练习是提高技能的有效方法,设计一些有趣的游戏或活动来增加学习的趣味性,如“数学接龙”、“家庭算术竞赛”等。
- 复习与反馈:定期复习已学内容并给予学生反馈是巩固记忆、纠正错误的重要手段,鼓励学生提出问题并解释其疑惑,这有助于加深理解。
- 实际应用场景:鼓励学生将所学知识应用于实际生活中,如家庭预算分配、厨房测量等,使学习变得更有意义和实用。
掌握除法竖式计算过程不仅是学习数学的需要,更是培养逻辑思维和问题解决能力的关键步骤,通过系统的学习和大量的实践,每个人都能成为除法计算的“小能手”。

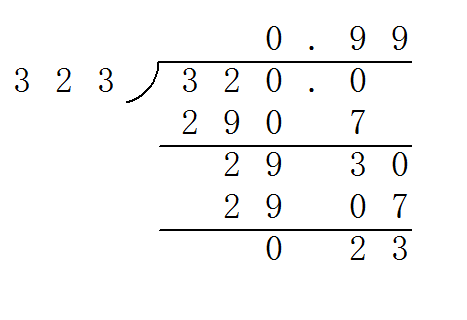

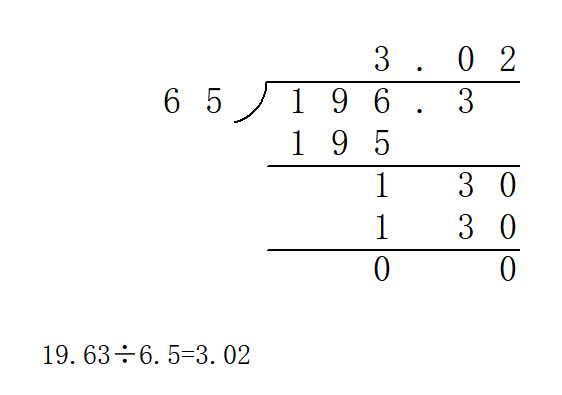
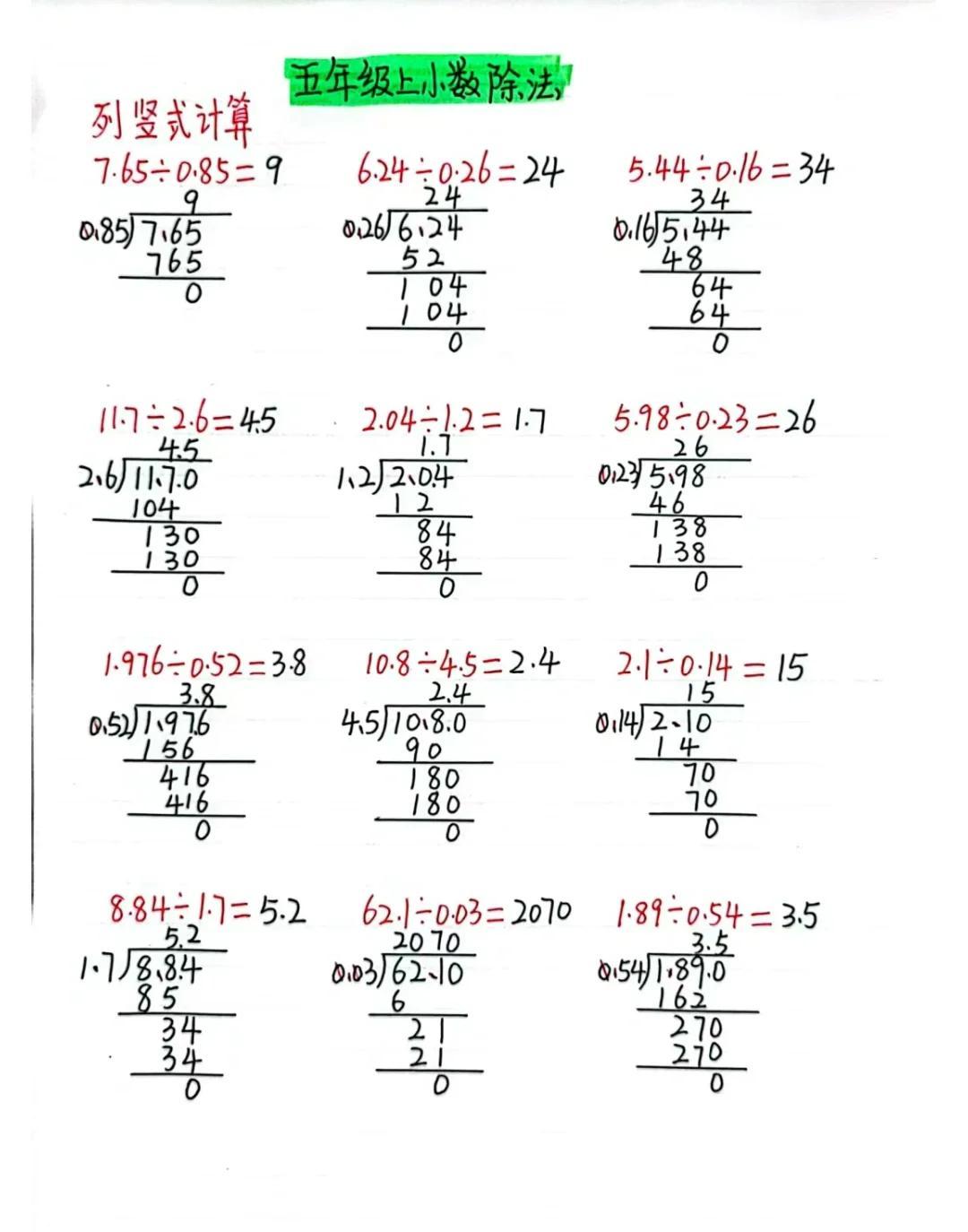
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号