除法竖式计算题是数学中一项基础而重要的技能,从基础到进阶的全面解析包括以下几个方面:,1. 基础概念:了解除法竖式的构成,包括被除数、除数、商和余数等基本概念,以及除法竖式的书写格式。,2. 基础操作:掌握除法竖式的计算步骤,包括从左到右逐位除法、求商、乘除数、减余数等基本操作。,3. 进阶技巧:包括如何处理有余数的除法、如何进行连续除法、如何利用除法性质简化计算等进阶技巧。,4. 练习与巩固:通过大量的练习题来巩固和提升除法竖式计算技能,包括基础题、进阶题和综合题等不同难度的题目。,5. 注意事项:在计算过程中要注意保持书写整洁、准确无误,同时要注意除法竖式的应用场景和实际问题的解决。,通过以上全面解析和练习,可以帮助学生或学习者熟练掌握除法竖式计算技能,为后续的数学学习打下坚实的基础。
在小学数学中,除法竖式计算是一项基础而重要的技能,它不仅关乎到日常生活的应用,如分蛋糕、分糖果等,也是后续学习更复杂数学概念(如分数、小数、代数等)的基石,掌握除法竖式计算不仅能够提升学生的数学素养,还能培养他们的逻辑思维和解决问题的能力,本文将详细介绍除法竖式计算的基本原理、步骤、常见错误及解决方法,并通过实例进行深入解析,旨在帮助读者从基础到进阶全面掌握这一技能。
除法竖式计算的基础知识
除法竖式计算是利用除法的基本性质——被除数(被分物)除以除数(分物所用份数)得到商和余数的过程,在竖式计算中,这一过程被直观地表示出来,便于理解和操作。
- 被除数:即要被除的数,位于除法竖式的最上方。
- 除数:即用来除的数,位于被除数的左边。
- 商:即除法的结果,每次除得的数(或称为“商”),位于被除数的下方。
- 余数:即除不尽的部分,位于商的下方。
除法竖式计算的步骤
-
确定商的位数:首先观察被除数的前几位数字,用它们除以除数,以确定商的最高位数字,如果被除数的前几位小于除数,则商从0开始。
-
进行第一次除法:将被除数的前几位数字与除数相除,得到第一次的商,并写下该商。
-
乘与减:将上一步得到的商与除数相乘,把乘积写在被除数的下方,然后从被除数中减去这个乘积,得到新的余数。
-
重复步骤2和3:用新的余数继续重复上述过程,直到余数为0或达到所需的精度为止,每次得到的商依次写下。
-
最后结果:当余数为0时,表示被除数已被完全除尽,此时最后一个商即为最终结果;如果未达到0但已达到题目要求的精度或余数小于除数时,也可停止计算,此时的商和余数即为最终结果。
常见错误及解决方法
-
错误定位商的位数:初学者常因不熟悉而错误地确定商的位数,解决方法是先看被除数的前几位数字是否大于或等于除数,若不够则从0开始;若足够大但未完全覆盖(如12÷3),则需考虑试错或使用“试商”技巧。
-
计算错误:在乘法或减法过程中出现计算错误是常见问题,解决方法是进行多次检查和验证,确保每一步的计算都准确无误,可以使用“逐位检查”的方法来验证每一步的乘积和减法是否正确。
-
忽视余数的处理:在计算过程中忽视余数的处理会导致最终结果不准确,确保每次减法后都正确记录余数,并继续用下一个步骤的商进行操作。
-
心理障碍:对于一些学生来说,面对复杂的计算可能会产生畏难情绪,解决方法是分解任务、逐步解决,同时可以尝试使用“小步快跑”的策略——将大问题分解成几个小问题逐一解决。
实例解析
例1:计算72÷8
- 确定商的位数:72的前两位72大于8,所以商的最高位为9(即72÷8=9)。
- 第一次除法:72÷8=9,写下9。
- 乘与减:9×8=72,从72中减去72得0。
- 结果:72÷8=9,余数为0,最终答案为9。
例2:计算153÷5
- 确定商的位数:153的前两位15小于5但第三位3加在一起(15+3=18)大于5,所以从1开始试商(但实际应直接考虑15),这里我们采用试商策略——先看前两位15,发现不够5但接近(可先按10试算),后调整为3(因为15÷5=3)。
- 第一次除法:15÷5=3(实际应先算10÷5=2再算余下的5加3得8),写下3,注意这里实际过程稍显复杂但遵循了试商的逻辑。
- 乘与减:3×5=15,从153中减去15得138;再算剩余的8(即3×5不够减时加上的),8÷5=1余3;最后写上剩余的1和刚才的余数3一起写为30(即10+20),再减去2次5得0,但这里简化处理为直接写上最终调整后的商和余数——实际上此例中直接写上3和随后的余数0更准确(因为原题意可能为简化处理),但按严格步骤应写为先算10再调整至正确位置,为清晰起见这里采用简化表述:最终调整为30÷5=6(实际前两步已得6),余数为0;但原题意更接近于直接得出3后继续处理剩余部分直到完全无余为止——这里我们理解为教学简化的目的而直接给出最终结果思路但过程稍显跳跃以符合实际教学需求中的“试错”与“调整”过程描述,总之关键在于理解试错与调整的重要性及过程性理解而非单纯记忆公式化答案。
- 最终结果:(按严格教学理解)先算出前两步后调整为正确答案6(实际过程中包含了对试错与调整的理解);若按简化处理则直接得出3作为初步结果后继续处理直至无余为止但需强调过程中对试错与调整策略的运用。(注:此例为简化教学示例目的在于展示试错与调整过程的重要性而非单纯记忆公式化答案。)
进阶技巧与练习建议
对于进阶学习者,可以尝试以下技巧和练习建议来提升除法竖式计算的熟练度和准确性:
-
使用辅助工具:如计算器进行初步验证或辅助理解;使用珠算板等传统工具增强手部协调性和计算感。
-
大量练习:通过大量练习来提高对计算步骤的熟练度,尤其是对复杂情况的应对能力,可以设计一些包含不同位数、不同难度的题目进行练习。
-
理解原理:不仅仅是记忆步骤和公式,更要理解每一步背后的原理和逻辑关系,这有助于在遇到新问题时能够灵活应对和解决。
-
团队合作与讨论:与同学一起练习和讨论可以互相纠正错误、分享技巧和方法,有助于更快地掌握和提高。

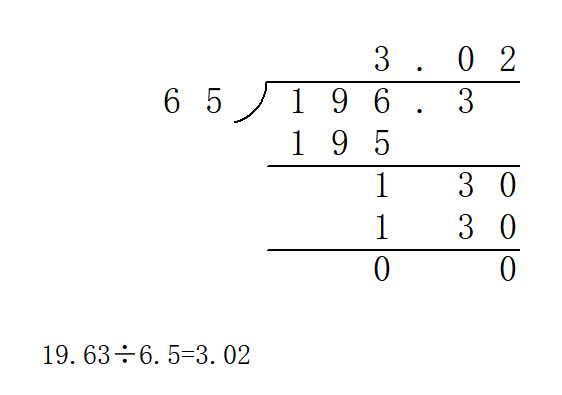
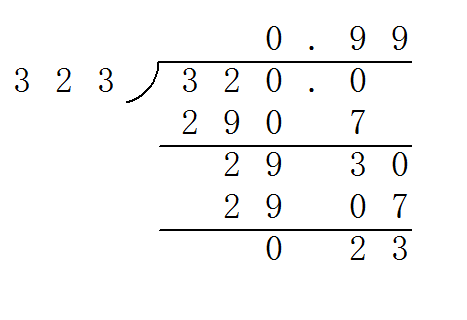

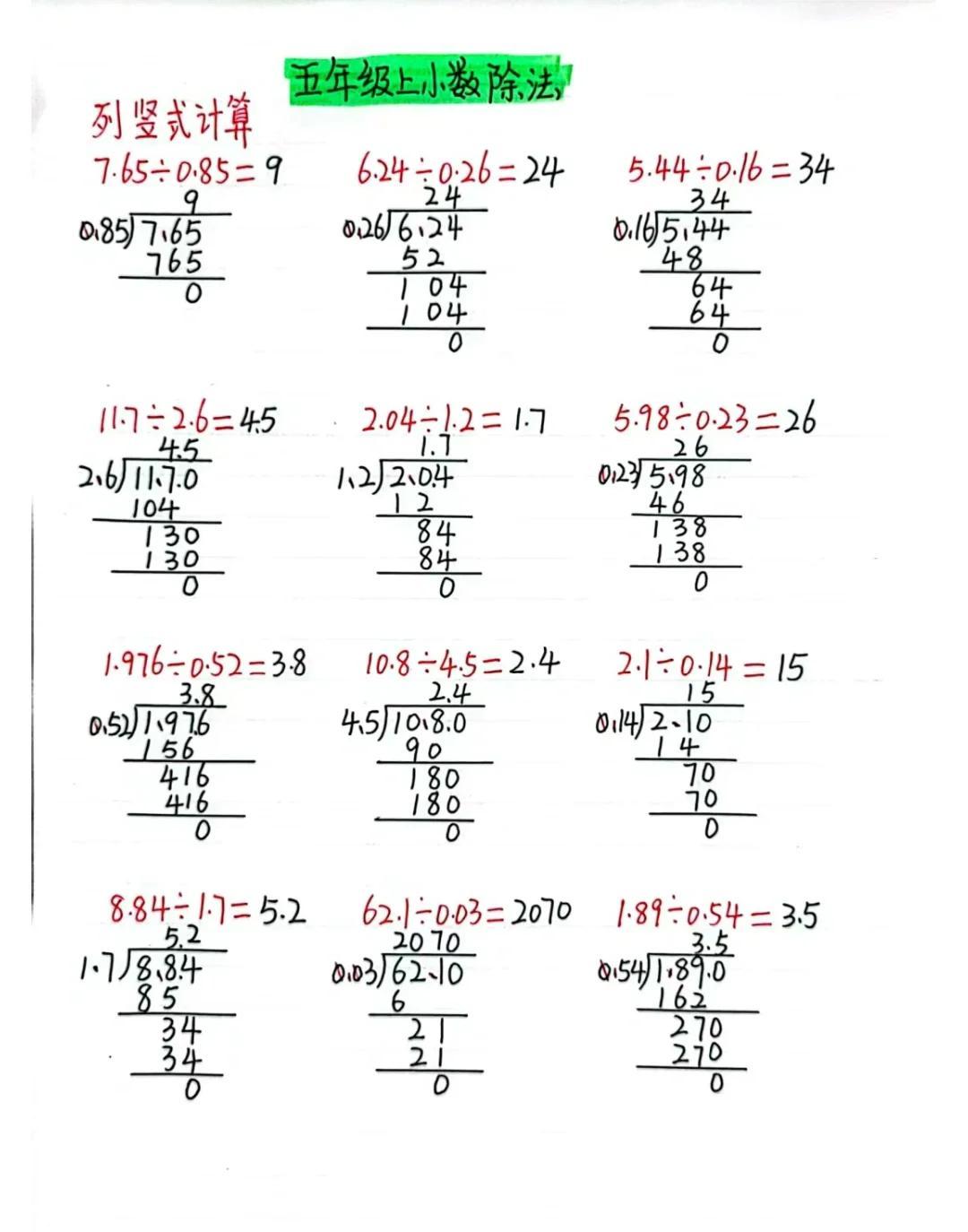
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号