除法竖式计算图是数学中一种重要的计算工具,它通过将除法运算过程以直观的方式呈现出来,帮助学生理解除法的基本原理和步骤,通过除法竖式计算图,学生可以清晰地看到被除数、除数、商和余数之间的关系,从而更好地掌握除法运算的技巧和规律。,使用除法竖式计算图,学生可以逐步理解除法运算的每一步骤,包括试商、除、乘、减等操作,这种直观的呈现方式有助于学生建立数学概念,提高他们的数学思维能力,通过反复练习和运用除法竖式计算图,学生可以加深对除法运算的理解和记忆,提高计算的准确性和速度。,除法竖式计算图是解锁数学奥秘的钥匙,它不仅帮助学生掌握除法运算的基本技能,还培养了他们的数学思维能力和解决问题的能力。
在数学的浩瀚海洋中,除法作为基础运算之一,其重要性不言而喻,它不仅是日常生活中的实用技能,也是更高层次数学学习的基石,对于初学者而言,除法概念的理解与实际操作往往显得既抽象又复杂,幸运的是,除法竖式计算图作为一种直观的教学工具,为这一难题提供了有效的解决方案,本文将深入探讨除法竖式计算图的应用、原理及其在数学学习中的重要性,旨在帮助读者更好地掌握这一数学技能。
除法竖式计算图的基本构成
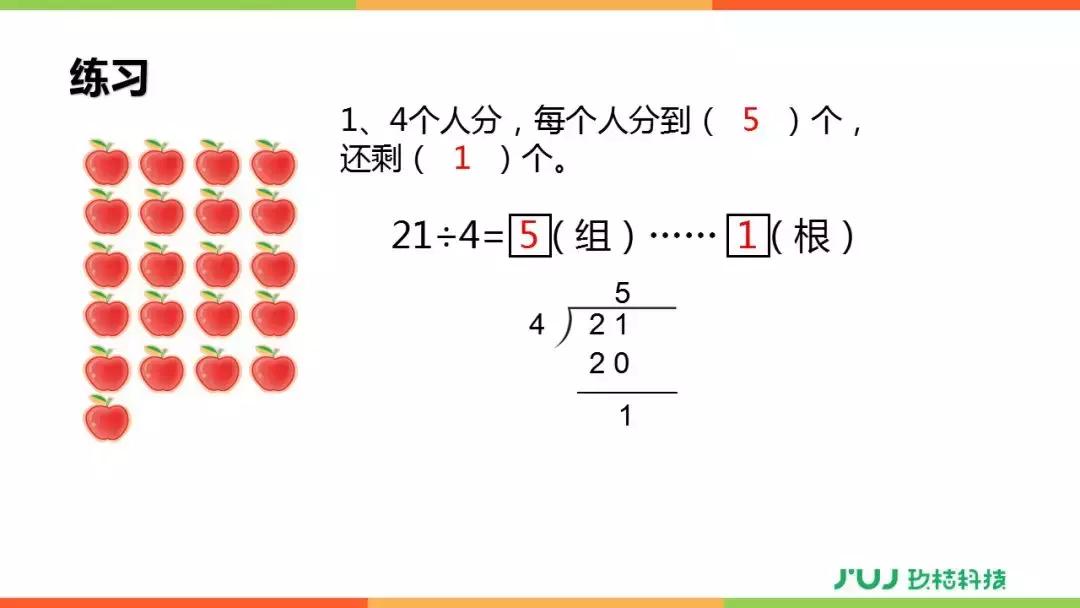
除法竖式计算图,顾名思义,是一种通过垂直排列的数字和运算符号来展示除法运算过程的图表,它主要由被除数、除数、商、余数以及除法过程中的每一步骤组成。
- 被除数:位于除法竖式的最左侧,是被分割的数。
- 除数:位于被除数的右侧,是执行分割操作的数。
- 商:在除法过程中逐步形成,位于被除数下方,代表每次分割后得到的整数部分。
- 余数:每次分割后剩余的数,位于商的下方,表示无法被完全除尽的部分。
除法竖式计算图的步骤解析
- 确定商的最高位:观察被除数的前几位数字,用它们除以除数,得到的商作为最高位。
- 乘除数并加至被除数:将上一步得到的商与除数相乘,将结果加在被除数的相应位置上。
- 重复上述过程:将上一步的结果再次与除数进行除法运算,得到新的商和余数,继续在竖式中记录。
- 继续直至无余:重复上述步骤,直到余数为0或达到所需的精度为止,如果余数不为0且继续进行会涉及小数或循环小数的情况,则根据需要进行取舍或说明。
除法竖式计算图的教学价值
- 直观易懂:通过图形化的方式展示复杂的除法过程,使得抽象的数学概念变得具体可感,有助于学生理解并记忆。
- 培养逻辑思维:使用除法竖式计算图要求学生进行逻辑推理和步骤分解,有助于锻炼他们的逻辑思维能力和问题解决能力。
- 提高准确性:相比心算或口算,竖式计算能更有效地避免错误,因为它要求每一步都清晰可见且可验证。
- 适应不同层次的学习者:无论是初学者还是有一定基础的学生,都能通过调整被除数和除数的位数来适应自己的学习水平,实现个性化学习。
实际应用与挑战
在现实生活中,除法竖式计算图的应用广泛存在于日常购物、烹饪、科学实验等场景中,在购物时计算找零、在烹饪中均匀分配食材、在科学研究中处理实验数据等,随着科技的发展和计算器的普及,人们可能逐渐减少了手算的机会,这在一定程度上也减少了使用除法竖式计算图的机会,但作为教育者或家长,应意识到这种传统方法在培养孩子数学思维和基础技能方面的重要性,适时地引入并练习这一技能。
除法竖式计算图不仅是学习数学的一个重要工具,更是开启数学世界奥秘的一把钥匙,它通过直观的图形化方式,使复杂的除法运算变得简单易懂,有助于培养学生的逻辑思维和问题解决能力,在数字化时代背景下,我们更应珍惜并传承这一传统教学方法的价值,让它在现代教育中继续发光发热,通过不断的练习和探索,每个人都能成为自己思维宫殿里的建筑师,用数学知识构建起通往智慧之门的桥梁。

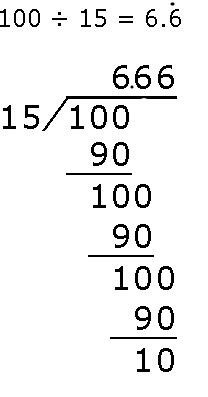
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号